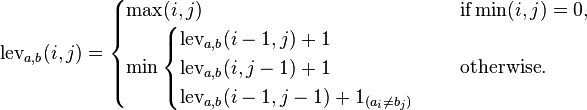title: 使用莱文斯坦距离（Levenshtein distance）计算两数组的差异
tags: [algorithm, javascript]
date: 2014-10-21 21:40:04

—

前言

莱文斯坦距离(Levenshtein distance以下简称ld)是一种常见的算法或可以称之为一种度量单位(前提是操作权重确定)，它用于表示从字串序列A到字串序列B所需要进行操作(增加、删除、更新)的综合。

鉴于数组与字符的相似性，这个算法当然同样适合与数组

问题是作为一个前端开发，你不好好切图，用这个算法做啥？

事实上Regularjs内部就使用到了这种算法，它用于检测数组的变动差异，并将差异反映到View中(即Dom)。

ld算法的另一个好处是，可以容易的将计算结果映射到未来将会到来的JS ES6Array.observe的返回值形式，方便未来的无缝迁移。

原理描述

ld算法

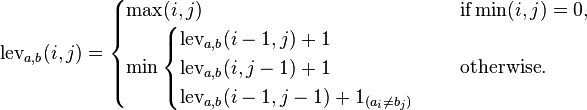
上图从Wiki上引用，它表示了LD距离的计算的基本原理，事实上我们需要提取编辑路径，这样我们才可以映射到具体的路径操作(比如更新dom).

在执行ld算法后，我们可以得到这样的二维矩阵

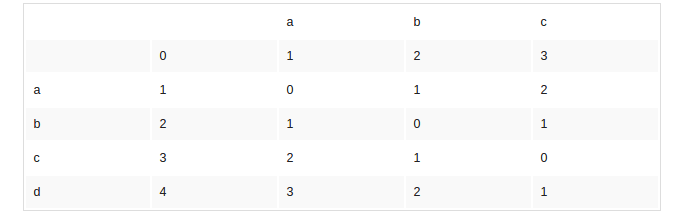
ld table

生成的矩阵的最后一个单元格, 即代表LS计算距离，这里从最后一个单元格回溯，我们就可以获得到从字符串A到字符串B的操作步骤，其中各个方向代表的含义是：

  1. 左上角: 不变或者替换（根据ld距离是否改变）
  2. 直左：代表删除一个字符
  3. 直右： 代表增加一个字符

具体路径选择根据特定环境而定 比如我们由于后续要用于dom更新的特点，我们需要保留的原对象越多越好。

【一知半解？戳这个demo】

See the Pen GnkAC by leeluolee (@leeluolee) on CodePen.

你可以手动输入字符串1和字符串2，由于使用了Regularjs，结果会实时响应。

javascript实现源代码

说明

  1. diff用来生成首次路径matrix
  2. whole函数用来回溯路径matrix，选择最合适路径
  3. 这里除了算法本身，还引入了转换数据格式的逻辑，方便后续操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
var ld = (function(){
  // 代表判定两者是否相等依据，这里我们认为 ===
  function equals(a,b){
    return a === b;
  }
  // 计算
  function diff(array1, array2){
    var n = array1.length;
    var m = array2.length;
    var matrix = [];
    for(var i = 0; i <= n; i++){
      matrix.push([i]);
    }
    for(var j=1;j<=m;j++){
      matrix[0][j]=j;
    }
    for(var i = 1; i <= n; i++){
      for(var j = 1; j <= m; j++){
        if(equals(array1[i-1], array2[j-1])){
          matrix[i][j] = matrix[i-1][j-1];
        }else{
          matrix[i][j] = Math.min(
            matrix[i-1][j]+1, //delete
            matrix[i][j-1]+1//add
            )
        }
      }
    }
    return matrix;
  }
  // 根据diff算法，回溯matrix，得到最后结果
  function whole(arr2, arr1) {
      var matrix = ld(arr1, arr2)
      var n = arr1.length;
      var i = n;
      var m = arr2.length;
      var j = m;
      var edits = [];
      var current = matrix[i][j];
      while(i>0 || j>0){
      // the last line
        if (i === 0) {
          edits.unshift(3);
          j--;
          continue;
        }
        // the last col
        if (j === 0) {
          edits.unshift(2);
          i--;
          continue;
        }
        var northWest = matrix[i - 1][j - 1];
        var west = matrix[i - 1][j];
        var north = matrix[i][j - 1];
        var min = Math.min(north, west, northWest);
        if (min === west) {
          edits.unshift(2); //delete
          i--;
          current = west;
        } else if (min === northWest ) {
          if (northWest === current) {
            edits.unshift(0); //no change
          } else {
            edits.unshift(1); //update
            current = northWest;
          }
          i--;
          j--;
        } else {
          edits.unshift(3); //add
          j--;
          current = north;
        }
      }
      var LEAVE = 0;
      var ADD = 3;
      var DELELE = 2;
      var UPDATE = 1;
      var n = 0;m=0;
      var steps = [];
      var step = {index: null, add:0, removed:[]};
      for(var i=0;i 0 ){ // NOT LEAVE
          if(step.index === null){
            step.index = m;
          }
        } else { //LEAVE
          if(step.index != null){
            steps.push(step)
            step = {index: null, add:0, removed:[]};
          }
        }
        switch(edits[i]){
          case LEAVE:
            n++;
            m++;
            break;
          case ADD:
            step.add++;
            m++;
            break;
          case DELELE:
            step.removed.push(arr1[n])
            n++;
            break;
          case UPDATE:
            step.add++;
            step.removed.push(arr1[n])
            n++;
            m++;
            break;
        }
      }
      if(step.index != null){
        steps.push(step)
      }
      return steps
    }
    return whole;
  })();

结尾

对一个正常人来讲，这种程度的算法都花不了你几个小时用来学习(更别说一些更常见的算法)，关键是要有这个意识它能用来解决什么实际问题，否则对数据结构与算法倒背如流都毫无意义。